Wisconsin algorithm Part 2

I have two comics to draw but on Friday, I was asked a question about Wisconsin’s “Sum to 1” algorithm (S1). I tried not to think about it, but then I had an idea while taking a shower. I didn’t have the time to check it out, but couldn’t get it out of my mind. Yesterday, I spent about 12 hours on it (and 6 on one of the comics).

The S1 algorithm is the most complicated one I’ve seen in four years of doing this type of research. The challenge of working on it is that it creates a data overload type of cognitive challenge. It is literally difficult to maintain a simultaneous mental image of its many components because there are so many, and they are spread out so far that it isn’t easy to create a visual reference.

If you read my paper on Wisconsin, you already have an idea what I mean. If you haven’t looked at it yet, here it is. For everyone else, here is the simple version:

At first glance, the S1 algorithm isn’t visible. If you sort the data at all, which is one of the first things anyone does when looking at data, the S1 is totally destroyed. For that reason, the data cannot be sorted until the row numbers in the original file are preserved. I learned to do this when studying the Spiral algorithm in NY, and have done it on every other state since.

For those of you with IT experience, the S1 sort is not an artifact of normal database usage by BOE personnel or standard optimization or save states. It is embedded in 7 snapshots of the data I’ve seen, covering a 2 year period, and it unnecessarily complicates the data. This strongly implies S1 is an engineered part of the database.

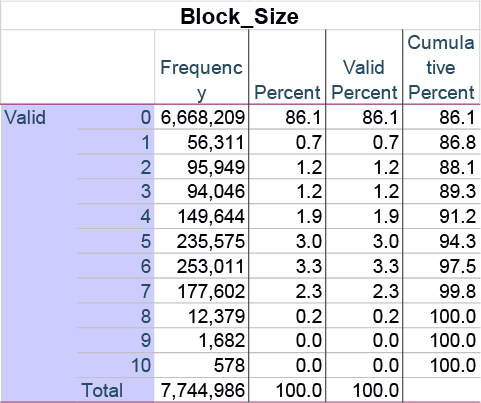
S1 affects about 5.5 million records of about 7.9 records in total. This is a continuous group of records that starts at about record number 1.6 million and ends about 500,000 records before the end of the file. This sandwiches S1 between two large groups of records that appear innocuous, effectively hiding it from casual observation.

To see it, one must calculate gaps between ID numbers, starting with the first S1 record. Then, add the gaps together, one after the other, until the cumulative total equals 1. Each group of records whose gaps sum to 1 (hence the name, S1) are what I call a ‘block’. Block sizes range from 2-10 records, with a block size of 6 being the most common.

Importantly, there are no disruptions in the run of about 5.5 Million S1 records. If there were, they would throw off the Sum to 1 constraint, and cause it to fail for all subsequent records. It is very sensitive to disruption. This is a huge sequence of numbers to match an artificial constraint like this, effectively eliminating the possibility this is chance.

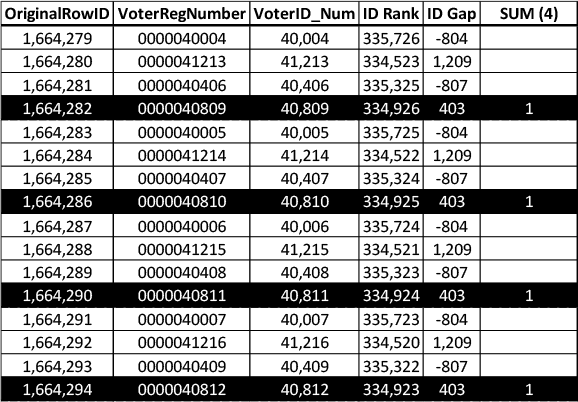
Here is an example:

Take a look at the ID Gap column. You will see that there are 4 blocks, each of size 4, and each with an identical block signature: -804, 1,209, -807, 403. Note that the signature, if summed, equals 1. Now note that the original RowID is consecutive, with no missing values. This should tell you that the S1 constraint only appears in this order. Then look at the VoterID_Number and do the addition yourself. You’ll see it works as described.

Now ask yourself, how is this done? How did these numbers get in this order? This is where the cognitive load becomes a heavy burden. There are over 34,000 signatures like these in Wisconsin. It doesn’t just have the signature shown here, it has over 34,000 more of them. Each represents a different combination, and the combinations themselves range from 2-10 different numbers. How does it decide to use one signature over another, and why?

If you go back to the example provided above, the first ID is 40,004. To get there, it had to go backwards -804 from the previous number (not shown) 40,808. In a normal database, the next ID would be 40,809, not 40,004. After 40,004, it goes all the way to 41,213. Put another way, 40,004+1,209. Why did it jump forward 1,209 places instead of 1? we know it isn’t random because it must sum to 1 by the end of the block.

To match the S1 constraint, the numbers in each block must have both positive and negative values, where the positive values add up to 1 more than the total of the negative values. To do this, there must be reserved numbers to allow numbering to go backward. This is not only enormously complicated, but it is made even more complicated by the fact there are over 34,000 signatures.

Let’s use a simple example with the sum to 1 constraint:

First ID= 1
Second ID = 10 (+9)
Third ID = 2 (-8)
Fourth ID = Cannot compute because the first 2 gaps already sum to 1, so a third cannot sum to the same value

Let’s try again:
First ID= 7
Second ID = 8 (+1)
Third ID = 1 (-7)
Fourth ID = Cannot compute because a +7 gap is needed, but that would make the fourth ID 8, the same as the second ID. Overlapping numbers isn’t allowed, so this doesn’t work either.

Let’s try again:
First ID= 2
Second ID = 10 (+8)
Third ID = 5 (-5)
Fourth ID = 3 (-2)

This works. Now imagine doing this with 34,000 different signatures for 5.5 million records, where some of the gap values are in the millions. Why were these specific values chosen? Was it trial and error, as in my example? If so, this is very computationally intensive.

It seems to me it would be easier if all the S1 numbers, those already assigned and those yet to be assigned, were pre-calculated, then handed out as needed. However, even that is very complicated and time intensive. Why someone would do this is puzzling, but my concern today is to figure out how it was done by solving the algorithm. Yesterday, I learned two new things that get me a little closer to the goal.

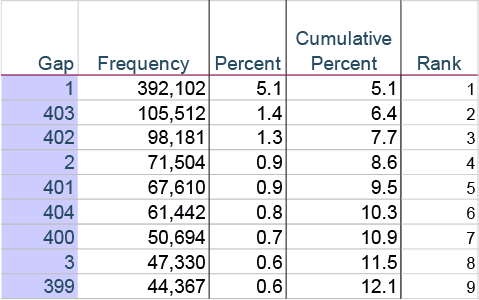
The first is that if you sort by ID number, then compare the row number for each, something interesting happens. The gaps between rows favor numbers near to, or multiples of, 400. The gap of 403 is the second most common after 1, with 105,512 instances, or 1.7% of all 56,318 gaps. Gaps of one are only found in non-S1 numbers, so they don’t count.

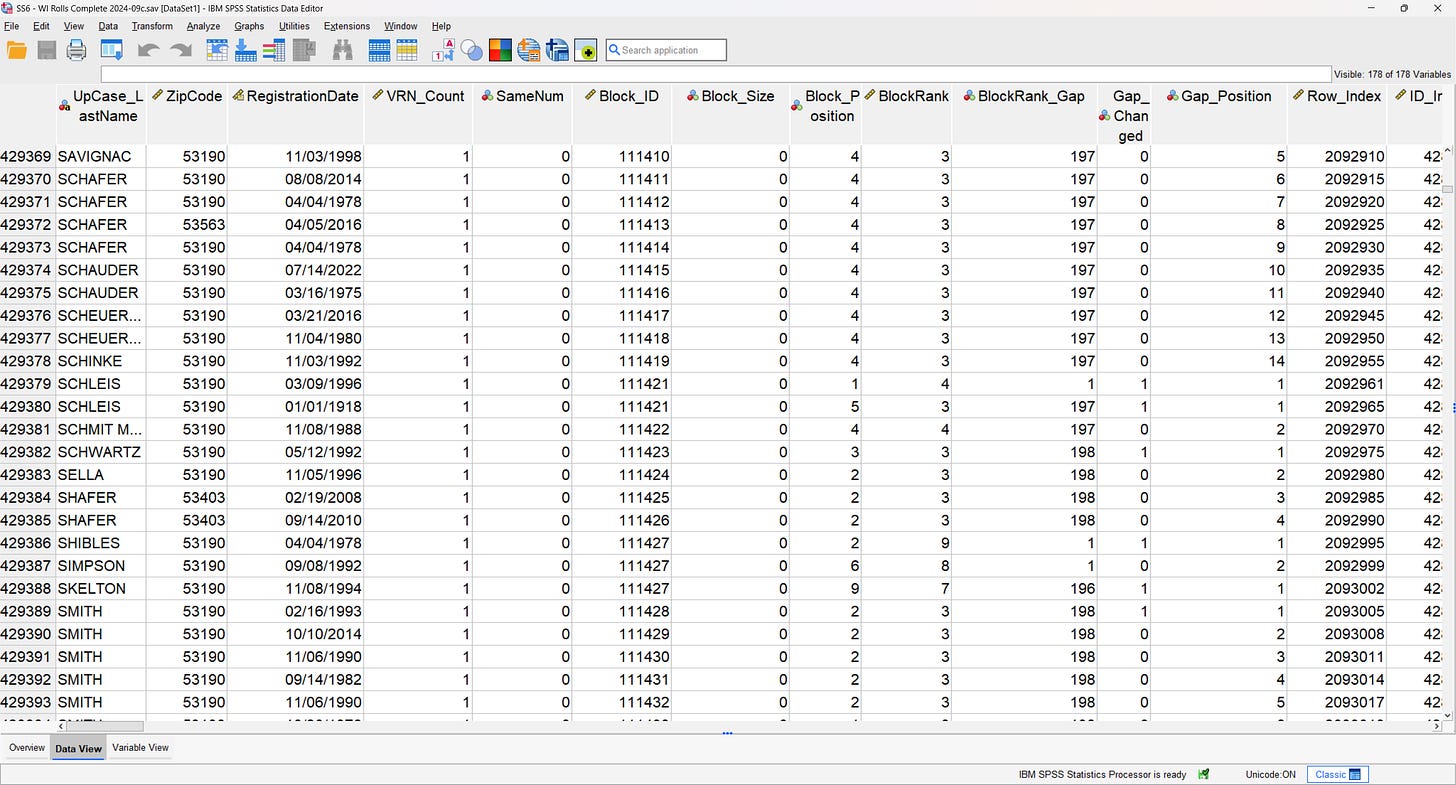
This is what they look like in situ:

The BlockRank_Gap is calculated based on the ID_Index, which is the row position of each record when sorted by ID. This tells us the row offset for each id.

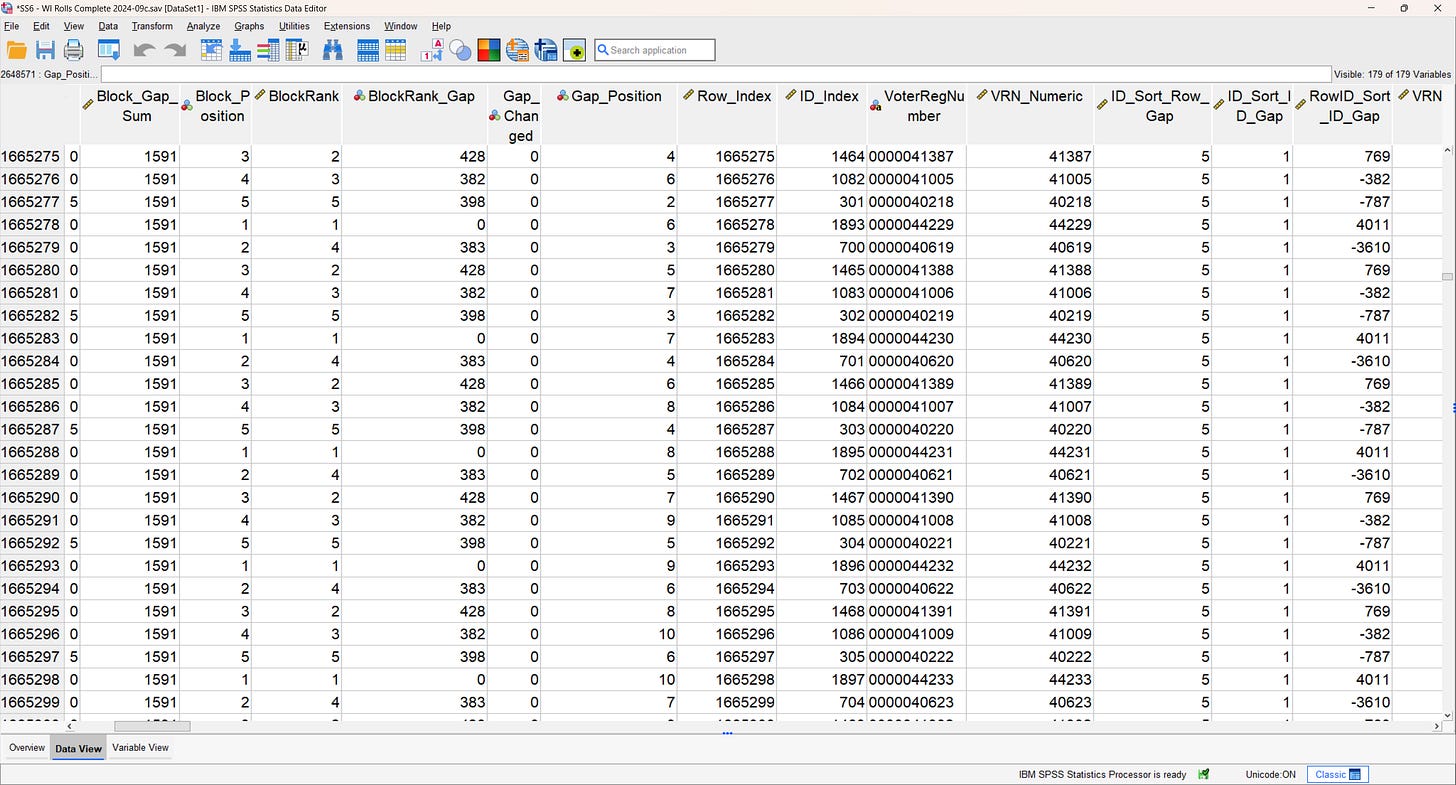
This tells us that as numbers increment by 1, they are displaced within the file by a value that is more often than not, close to 400 rows.

The next bit of information is that if the BlockRankGaps are summed on a per-block basis, we can see the total row displacement within the block. In the illustration above, it is 1591 rows (close to 1600, or 4*400). However, over the full set of S1 numbers, the range of gap sums varies from 2 to 4,936,261. This means the S1 constraint is manipulating a very wide range of numbers to achieve its goal. It also tells us that the effective flexibility of the algorithm so far does not extend beyond 7 digit numbers. Meaning, it isn’t infinite. It also means that the number space is more tightly packed than it could be, and that makes it even more difficult to achieve the precise S1 constraint.

The S1 algorithm's characteristics fundamentally violate principles of standard database management: no legitimate administrative process requires 34,000+ variable-length sequences to sum to precisely 1, particularly when achieving this constraint demands computationally intensive backward number reservation across millions of records with gaps extending into the millions. The pattern's persistence across seven database snapshots over two years, its destruction under any standard sorting operation, its sandwich architecture between "normal" partitions, and its systematic 400-multiple row displacement patterns represent a level of mathematical precision and algorithmic sophistication that serves no documented administrative purpose. Standard voter registration databases prioritize sequential assignment, data integrity, and operational simplicity—the S1 implementation achieves the opposite through unnecessary complexity that requires significant computational resources and advance planning, creating a system so sensitive to disruption that a single sequence error would cascade through 5.5 million records, yet it maintains mathematical perfection across this massive dataset.

Anyway, I shouldn’t be working on this right now. I have to get back to the Korean War. Just wanted to share what is going on this Sunday.